先来看这样一道资料分析真题：

　　2010年上半年，全国原油产量为9848万吨，同比增长5.3%，上年同期为下降1%。进口原油11797万吨，增长30.2%。原油加工量为20586万吨，增长17.9%，增速同比加快16.4个百分点。成品油产量中，汽油产量增长6%，增速同比减缓7.9个百分点;柴油产量增长28.1%，增速同比加快15.8个百分点。

　　2010年上半年全国原油产量比2008年同期增长了约：( )

　　A.1.8% B.4.2% C.6.3% D.9.6%

　　这是一道很典型的两期间隔增长率题目，问题问2010年相对于2008年的增长速度是多少，2010年和2008年是非常明显的两期年份，中间间隔了2009年一年，对于这种题目我们直接套用两期间隔增长率公式，就可以非常便捷的解出答案。

　　根据题意，所以选择B选项。

　　这道题目的特征十分明显，我们可以很轻易地发现这是使用两期间隔增长率公式的题目，也就是说，我们在解题时，先观察问题中的时间，再对照资料的时间，就可以很快确定是否需要使用两期间隔增长率公式。实际上两期间隔增长率公式的用处就像比重变化的知识点一样，不仅仅局限于时间，还有一部分其他题目，也是可以运用这个公式进行求解的，例如下面这类题目。

　　2008年，我国粮食种植面积达到10670万公顷，增长1.00%，粮食单产4.95吨/公顷，增长4.21%。请问我国2008年粮食总量增长率为多少?( )

　　A.5.17% B.5.21% C.5.25% D.5.31%

　　题目让我们求解粮食总量的增长率，而材料当中并未给出粮食总量的现期值和基期值，给出的是粮食种植面积和单产量，那么很明显有关系式：粮食总产量=单产量总面积。根据公式我们可以得出现期值=，基期值，带入增长率的公式得到本题的算式为：

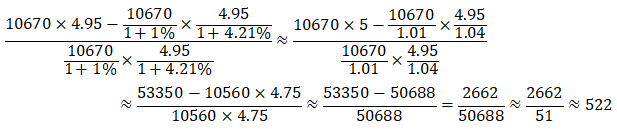
　　观察题目四个选项可以发现，这道题目的选项差距较小，计算需要保证一定的精确度，解这个式子为：

　　所以选择B选项。

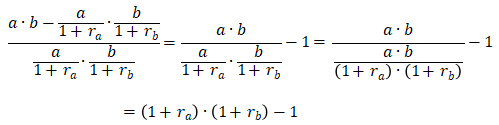
　　这道题我们结合了多种方法去计算，最终得出了答案。但是在求解的过程中，我们很明显的会感觉到计算十分的繁琐复杂，观察发现这个算式是具有一定特点的，那么我们不妨来对整个式子进行化简，来寻找其中的规律。同样，为了方便观察，我们用和分别表示粮食种植面积和粮食单产量，和分别对应两者的增长速度，那么，这道题的算式就可以改写为：

　　展开这个式子得到如下的公式：

　　这个式子和两期间隔增长速度公式完全一样，将资料中的数据带入式子中进行验证如下：

　　验证发现，计算得到的结果和直接计算一致，这说明，像这类题目也可以运用两期间隔增长率公式。

　　那么这类题目有什么特征呢?我们来对比一下两者最初的式子有什么区别：

　　【式子1】两期间隔增长速度：

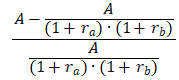
　　【式子2】

　　观察可以发现所求问题是、两者之积作为一个整体来计算增长率，也就相当于两期间隔增长率中的。

　　所以说两期间隔增长速度公式可以运用于以上两种情况。