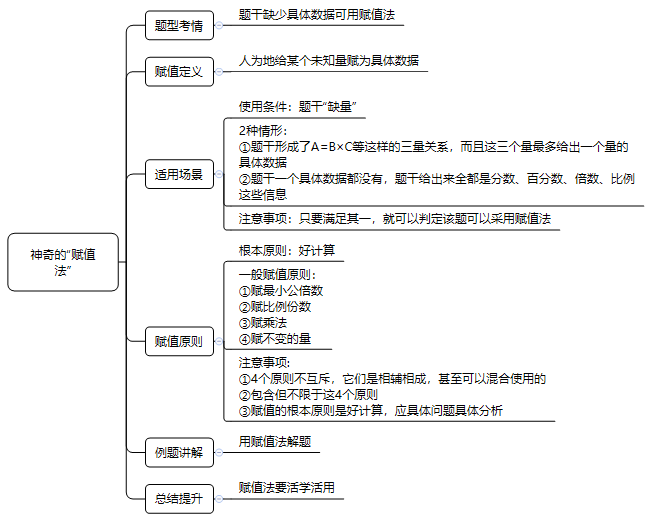
数学运算中经常会遇到一种题目，它的题干没有给出具体数据的时候，题目问的也是相对情况，对于这样题，很多考生都会纳闷，题干都没有给，我们怎么求?其实，遇到这类题，考生不必感到慌张，因为，此类题目可以通过“赋值法”来快速破题。接下来本文将详细介绍此类题目的解题方法“赋值法”。

　　1.“赋值法”的定义

　　赋值法是一种解题思想，那么它是一种什么样的思想呢?所谓的“赋值法”就是人为地给某个未知量赋为具体数据。那么，我们就有必要明确何为具体数据，具体数据是指带单位的数据，如50万元就是具体数据，又比如1/3，它没有单位，所以不能称之为具体数据。

　　2.“赋值法”的适用场景

　　赋值法虽然可以人为地给某个未知量赋为具体数据，但是赋值法也不是随时随地随心所欲地使用，要采用赋值法就必须要满足题干“缺量”这么一个条件，而“缺量”具体体现在以下两种情形。

　　①题干形成了A=B×C等这样的三量关系，而且这三个量最多给出一个量的具体数据。如工程问题中，存在“总量=效率×时间”这样的三量关系，如果题目只给出时间，效率和总量并没有给出，则满足“形成了A=B×C的三量关系，而且这三个量最多给出一个量的具体数据”，则可用赋值法。

　　②题干一个具体数据都没有，题干给出来全都是分数、百分数、倍数、比例这些信息。

　　需要注意的是，以上两种情形，只要满足其一，就可以判定该题可以采用赋值法。

　　3.“赋值法”的赋值原则

　　在确定可以采用赋值法之后，接下我们就要思考怎么赋值才能更有利于解题。赋值的目的是为了帮助我们解题，那么解题时我们也希望计算简单，因此，在赋值时我们要遵循一个根本原则——好计算，人为赋予的数据应该让该题的计算简单、容易。一般来说好计算可以体现在在4个原则：

　　原则一：赋最小公倍数

　　原则二：赋比例份数

　　原则三：赋乘法

　　原则四：赋不变的量

　　这4个赋值原则，我们需要注意3点，一是这4个原则不是互相排斥互相独立，它们是相辅相成，甚至可以混合使用的;二是赋值原则包含但不限于这4个原则;三是赋值的根本原则是好计算，所以在赋值时应该具体问题具体分析，而不是刻板的使用所谓的赋值原则。

　　4.例题讲解

　　【例1】某楼盘的地下停车位，第一次开盘时平均价格为15万元/个;第二次开盘时，车位的销售量增加了一倍、销售额增加了60%。那么，第二次开盘的车位平均价格为：

　　A.10万元/个B.11万元/个

　　C.12万元/个D.13万元/个

　　【答案】C

　　【解析】根据题干形成“销售额=平均价格×销售量”的三量关系，这三量关系中只有平均价格是具体数据，因此可用赋值法解题。因为题目给出第一次开盘的平均价格为15万元/个，因此赋第一次开盘的销售量为1个，则第一次开盘的销售额为15×1=15万元。根据题干信息“第二次开盘时，车位的销售量增加了一倍、销售额增加了60%”，可求第二次开盘的销售量=1×2=2个，销售额=15×(1+60%)=24万元，则根据公式平均价格=销售额÷销售量=24÷2=12万元/个。因此选择C选项。

　　【例2】高架桥12：00～14：00每分钟车流量比9：00～11：00少20%，9：00～11：00、12：00～14：00、17：00～19：00三个时间段的平均每分钟车流量比9：00～11：00多10%。问17：00～19：00每分钟的车流量比9：00～11：00多：

　　A.20%B.30%

　　C.40%D.50%

　　【答案】D

　　【解析】已知题干给出的信息全是百分数，一个具体数据都没有，因此可用赋值法解题。赋值9：00—11：00每分钟车流量为10，则12：00—14：00每分钟车流量为10×(1-20%)=8，三个时段每分钟车流量的平均值为10×(1+10%)=11。则17：00—19：00每分钟车流量为11×3-10-8=15。故17：00—19：00每分钟车流量比9：00—11：00多50%。因此，选择D选项。

　　通过上面的例子，我们发现遇到一些“缺量”的题目时可以采用赋值法，赋值法也确实可以帮助考生快速破题。当然，赋值法也不是一成不变的，各位考生应该灵活应用，想要了解更多的赋值法内涵，各位考生可继续关注华图教育。